Manipulator

Posted in Robotics

Manipulator Simulations

6자유도 협동로봇의 Matlab 시뮬레이션

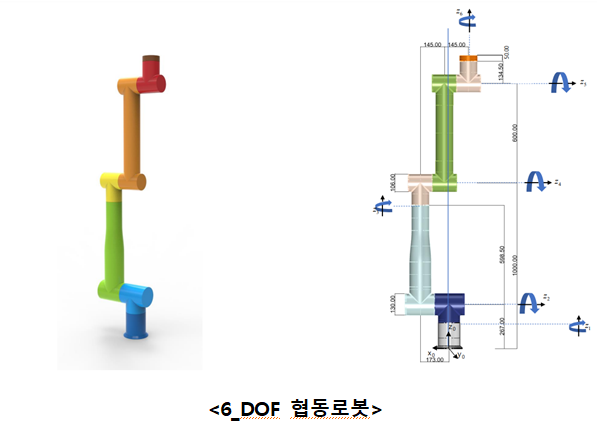
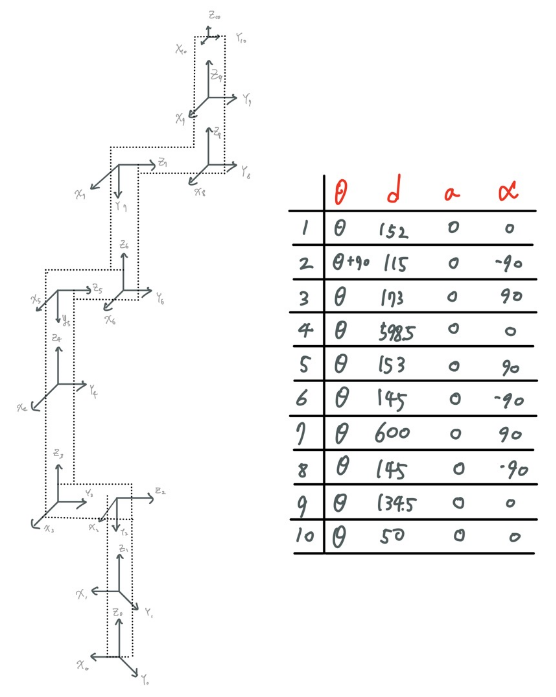
Ⅰ. D-H 파라미터

• D-H 파라미터는 기계 공학의 로봇팔과 같이 연결된 링크 간의 관계를 수학적으로 표현할 수 있는 기구학적인 모델링 방법을 활용한 매개변수이다. 총 4개의 매개변수가 있으며 각각의 매개변수는 링크의 좌표계 설정하여 두 개의 링크 간의 좌표계를 나타낸다. D-H 파라미터를 구하기 전에 좌표계를 설정한다. 조인트에서의 좌표의 원점을 Oi점으로 정한 후 각 조인트에서 움직이는 축을 중심으로 Z축을 설정한다. 로봇의 회전 축을 중심으로 Z축을 선정하는데 이 때 엄지손가락이 가리키는 방향이 Z축이며 오른손 법칙을 이용한다. Z축을 오른손법칙으로 선정하였을 때 검지 손가락이 가리키는 방향이 X축이며 이 X축은 Zi-1 축과 Zi 축에 수직인 평면으로 Zi-1에서 밖으로 나가는 방향으로 Oi를 지나 Zi 축에 수직하다. 이후 Y축은 Z축과 X축에 의해 오른손법칙으로 정해진다. D-H파라미터를 설정할 때 간편히 하기 위해 회전축이 없는 End_effector는 가능하면 이전 축을 기준으로 같은 방향으로 설정하는 것이 좋다. 좌표계가 설정되고 난 후 D-H파라미터를 구하기 위해서는 각 좌표축간의 관계를 파악해야한다. D-H파라미터는 d, θ, a, α 가 있으며 각각의 의미는 다음과 같다.

D-H 파라미터

• d : Zi 축을 기준으로 Xi 축 Xi+1 축 사이의 최단 거리

• θ : Zi 축을 기준으로 Xi 축 Xi+1 축 사이의 각도

• a : Xi 축을 기준으로 Zi 축과 Zi+1 축 사이의 최단 거리

• α : Xi 축을 기준으로 Zi 축과 Zi+1 축 사이의 각도

6 axis D-H parameters \[A_{i-1}^{i} = \left[\begin{array}{} cos(\theta_i) & cos(\alpha_i)sin(\theta_1) & sin(\alpha_i)sin(\theta_i) & a_icos(\theta) \\ sin(\theta_i) & cos(\alpha_i)cos(\theta_i) & -sin(\alpha_i)cos(\theta_i) & a_isin(\theta_i) \\ 0 & sin(\alpha_i) & cos(\alpha_i) & d_i \\ 0 & 0 & 0 & 1 \end{array}\right]\]

translation matrix

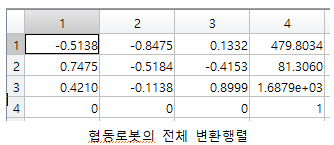
Ⅱ. 베이스좌표계$(x_{0},y_{0},z_{0})$로부터 End-effector까지의 천이행렬

좌표계를 설정하고 D-H 파라미터를 구한 후 Translation 행렬에 대입하여 T행렬을 계산한다. T행렬은 Rotation matrix와 Position matrix로 구성되어 있으며 Rotation matrix는 Roll, Pitch, Yaw의 방향으로 회전한 행렬을 모두 연산하여 3 x 3 행렬로 구성되고 Position matrix는 X, Y, Z로 3 x 1 행렬로 구성되어 있으며 차원을 맞춰주기 위하여 전체 행렬은 4 x 4 행렬로 구성한다. T행렬은 각 D-H파라미터를 대입하여 0번 조인트에서 1번 조인트까지의 관계, 1번 조인트에서 2번 조인트까지의 관계를 계속해서 나타내고 최종적으로 나타내고자하는 n-1번 조인트에서 n번 조인트까지의 관계까지 모두 계산한 다음 이런 T행렬을 T_0_1부터 T_n-1_n 까지의 곱으로 초기 좌표계에서 구하고자하는 End-effector까지의 관계(회전과 위치)를 구할 수 있다.

전체 변환 행렬 (은 n좌표에서 오리엔테이션 행렬, 은 n좌표에서 위치 벡터)

Ⅲ. 순기구학을 이용하여 각 링크의 관절각을 표현할 수 있는 Matlab 시뮬레이션 프로그램을 구현

• Matlab 시뮬레이션은 2개의 함수.m 파일과 3개의 실행.m 파일로 구성했다. 먼저 함수 파일의 theta.m 파일은 T행렬을 계산하기 위해 D-H파라미터를 대입할 수 있는 행렬을 함수로 나타내었고 ficture.m 파일은 D-H파라미터를 직접 입력해주고 theta.m 파일의 함수를 활용하여 plot을 띄우면서 각 링크, 조인트의 위치를 나타내고 End-effector의 위치 또한 추가적으로 좌표를 표시했다. DOF_6.m 파일은 ficture.m 파일의 기본적인 위치를 표시하기 위한 파일로 D-H 파라미터 중 변수인 θ1 부터 θ6 까지의 default 값을 0으로 지정하여 초기의 협동로봇의 위치를 나타내었다. DOF_6_exe.m 파일은 사용자가 직접 변수를 입력할 수 있도록 하였다. 먼저 사용자의 입력이 Y 또는 y이면 각 θn 에 동일한 값을 입력받고 반복횟수를 입력받아 전체적인 협동로봇의 형상이 초기상태부터 차례대로 진행되며 겹쳐보일 수 있도록 하였다. 사용자가 입력을 N 또는 n으로 입력하면 하나의 협동로봇의 형상만 표시하는 것으로 각각의 θn 값을 입력받아 θn 값에 의해 변하는 plot을 살펴볼 수 있도록 하였다. Fun_Link.m 파일은 line 5에 loop 값에 따라 달라지는 협동로봇의 형상을 표현한다. 링크와 조인트의 통일된 색상으로 DOF_6_exe.m 파일보다 조금 더 전체적인 로봇의 큰 틀의 형상을 살펴볼 수 있다. matlab에서 plot의 비율을 조정하기 위해 축의 범주를 한정해두면 협동로봇의 형태가 축의 범주를 넘어서면 표현되지 않는다. 각 매트랩파일에서 axis에 대한 설명부분을 주석처리하면 비율은 맞지 않으나 End_effector이 표현되지 않는 경우는 없다. (매트랩 결과로 출력된 좌표 중 –7.164e-15의 값은 실제 값은 0이다.)

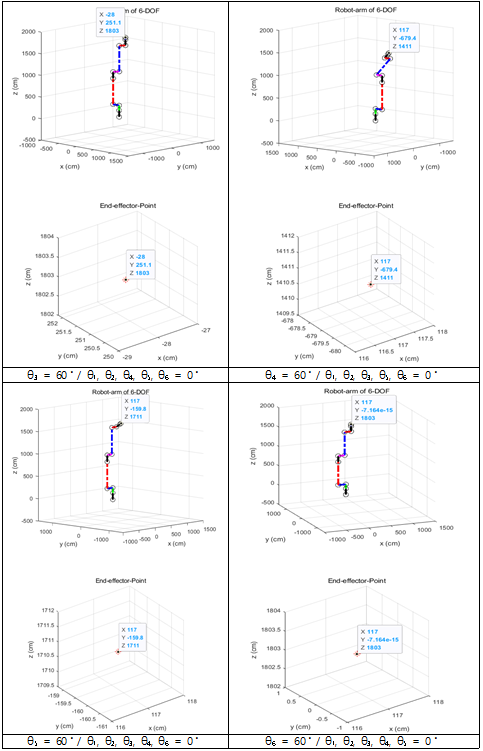
Matlab Simulation result

Matlab으로 구현한 시뮬레이션이 실제 계산결과와 동일한 결과를 출력하는지 검산할 필요가 있다. 따라서 시뮬레이션에서 대입한 θn = 60 로 설정하여 D-H파라미터 값으로 전이행렬을 옳게 출력하고 위치벡터(X,Y,Z)의 결과로 End-effector의 위치와 동일한 결과인지 판단한다. 예를 들어 θ2 = 60, θ5 = 60로 설정하여 검산과정을 진행한다.

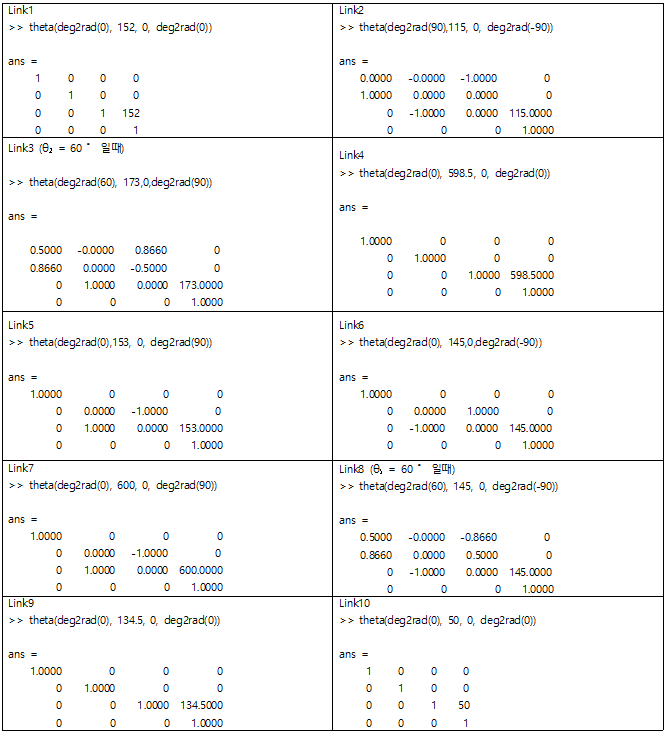
Link의 행렬들을 모두 연산하면 \[A = 10^3 \begin{bmatrix}0&-0.001&0&0.117 \\ 0.001 & 0 & 0 & 1.1704 \\ 0 & 0 & 0.001 & 1.1272 \\ 0 & 0 & 0 & 0.001 \end{bmatrix}\]

위치벡터의 값이 117,1170,1127이므로 End_effector의 좌표 (X,Y,Z) = (117, 1170, 1127)이다. 시뮬레이션 결과와 동일한 것을 확인할 수 있다.

Ⅴ. 경로계획 방법을 이용하여 로봇팔의 End-effector의 경로를 Cubic Spline 이용해서 작성

• path planning을 진행하기 위해서는 현재 위치와 도착 위치를 설정한 후 두 점을 잇는 경로를 계획한다. 두 점을 잇는 경로는 다양하며 로봇이 일반적으로 움직이는 경로를 설정할 때 도달시간이 빠르며 안정적으로 이동경로를 설정하여 도착 위치에 도달하는 것이다. 출발 위치와 도착 위치를 바로 잇는 직선이 가장 빠른 경로는 맞지만 실제 로봇의 이동경로를 두점을 잇는 경로가 항상 안정적으로 동작하는 것은 아니다. 실제 로봇의 이동경로를 PD제어를 통해 추종하는 프로그램을 진행할 때 이동 포인트를 정확히 통과하고 다음 이동 포인트로 방향각을 설정하기 위해 선회하는 것으로 나타난다. 마찬가지로 로봇팔에서도 포인트 이동에서 직선으로 바로 도달하는 것이 안정적이지는 않다.

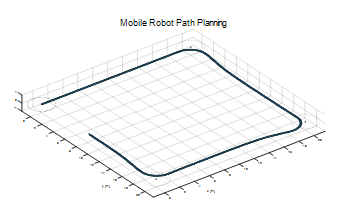
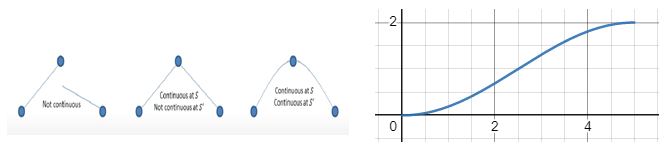
• 추가적으로 로봇이 이동할 때 정지, 등속, 정지의 과정으로 로봇이 작동하지 못한다. 따라서 실제로 로봇의 정지, 가속, 등속, 감속, 정지의 과정을 거치며 이동경로를 설정하고 부드러운 모션으로 진행할 수 있도록 하기 위해 Cubic Spline을 이용한다. Cubic Spline의 조건으로 로봇의 출발 위치에서 각도는 0이고 각속도 또한 0이다. 도착지점에서의 위치는 설정한 값이 존재하지만 마찬가지로 각속도는 0으로 설정된다. 아래의 왼쪽 그림과 마찬가지로 함수가 어느 한 점에서 불연속으로 진행할 수 없다. 이러한 조건을 만족 시키면서 가속, 감속 과정을 진행하기 위해서는 실제로 아래의 오른쪽 그림과 같이 X 축(시간축)에 대한 Y 축(각도)의 변화로 나타낼 수 있다.

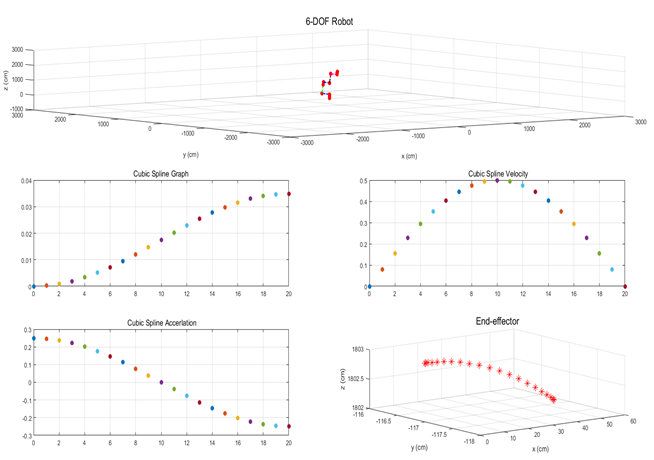
• 실제 시뮬레이션 결과 6자유도 협동로봇의 전체 형상 및 움직이는 각도는 θ3 값에 입력 값으로 진행하였다. Cubic Spline의 위치, 속도, 가속도를 그래프로 시간에 대한 변화를 나타내고 마지막 그래프에서는 End-effector의 위치를 나타냈다. Cubic Spline 함수는 아래와 같이 설정하였다.

\[\theta(t) = A(1-cos(\frac{n\pi}{T})t)\]

Ⅵ. 설정된 경로를 추종하는 관절각을 계산하는 역기구학 시뮬레이션 코드를 작성

• 역기구학은 로봇의 위치가 정의되어 있을 때 현재 로봇의 End-effector에서 θ의 값을 구하기 위해 End-effector의 위치에서 atan2의 함수를 이용해서 기울어진 각도를 반대로 계산해 나가는 과정이다. 이때 atan2를 활용하는 이유는 atan은 θ의 값이 0 ~ 2π으로 지정되어 있어 π의 값에서 tanθ의 값이 발산하는 결과가 발생하기 때문에 atan2는 θ의 값이 -π ~ π 으로 설정되어 tanθ의 값이 불연속인 구간이 없다.

\[A^i_i-1 = \begin{bmatrix}cos( \theta_i) & -cos(\alpha_i)sin(\theta_i) & sin(\alpha_i)sin(\theta_{i}) & a _{i}cos(\theta) \\ sin(\theta_{i}) & cos(\alpha_{i})cos(\theta_{i}) & -sin(\alpha_{i})cos(\theta_{i}) & a_{i}sin(\theta_{i}) \\ 0 & sin(\alpha_{i}) & cos(\alpha_{i} ) & d_{i} \\ 0 & 0 & 0 & 1 \end{bmatrix}\]

변환행렬에서 a의 값이 0이기 때문에 위치 벡터에서의 에서 tanθ의 값이 이기 때문에 값이 없어서 역기구학을 계산할 수 없다.