Coordinates

Posted in Mathematics

Coordinates System

• 좌표계는 로봇에서 움직이는 공간상의 위치를 나타내기 때문에 중요한 개념 중 하나이다.
• 로봇의 운동 제어, 위치, 임무 수행, 등의 다양한 작업 수행을 하기 위해서는 로봇의 현재 위치와 목표 위치를 정확히 인지하고 있어야한다.
• 이에 대한 정보의 부족으로 모바일 로봇의 충돌, 산업용 로봇의 안전 등 다양한 문제가 발생할 수 있다.
• 로봇에서 사용되는 좌표계는 다양한 좌표계를 사용하고 있다 좌표계의 종류, 차이점, 특성을 이해해보자.
• 또한 좌표계의 종류는 아니지만 Euler 각도에 대해서도 이해한다.

직교좌표계(Orthogonal coordinates)

데카르트 좌표계 (cartesian coordinate)

데카르트 좌표 = 카테시안 좌표는 기하학에서 공간 상의 점을 좌표로 나타내는데 가장 일반적으로 사용되고 있는 좌표로 지금까지 우리가 흔히 알던 기본적인 좌표계이다.

• 2차원 좌표계
  • 평면 상의 한 점을 나타낸다. 좌표계는 수평으로 x축, 수직으로 y축으로 이루어져 있다.
  • 점의 위치는 (x,y)로 나타낸다.
• 3차원 좌표계
  • 공간 상의 한 점을 나타낸다. 좌표계는 수평으로 x축, 수직으로 y축, 그리고 x,y 축이 이루는 평면에 수직인 z축으로 이루어져 있다.
  • 점의 위치는 (x,y,z)로 나타낸다.

극좌표계 (polar coordinate system)

극좌표계는 평면상의 한 점을 극, 방위각으로 점의 위치를 나타내고 데카르트 좌표계에서는 삼각함수를 사용해서 변환할 수 있다.

• 극(r) : 원점에서부터의 해당 점 사이 거리를 나타낸다.
• 방위각(θ) : x축의 양의 방향으로부터 시계 방향을 측정된 각도를 나타내며 단위로 (radian, degree)가 있다. (일반적으로 radian 단위를 사용함)

따라서 점의 위치가 (r,θ)로 나타나며 데카르트 좌표계로 변환하면 (r * cos(θ) , r * sin(θ)) 로 구성될 수 있다. 특징으로는 극좌표계는 원형 대칭 문제를 다루는데 효과적이며 중력, 전자기학 등 공학에서 자주 사용된다.

• 극좌표계에서 데카르트 좌표계로 변환시 :

$$\begin{gathered} x=rcos(\theta ) \\ y=rsin(\theta ) \end{gathered}$$

원통좌표계 (cylindrical coordinate system)

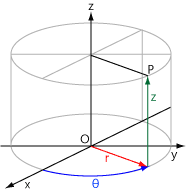
원통좌표계는 점의 위치를 원점과의 거리, 방위각, 그리고 높이로 표현하는 좌표계다.

• 극(r) : 원점으로부터 수평 거리를 나타낸다. 원점과 점 사이의 직선 거리
• 방위각(θ) : x축의 양의 방향으로부터 시계 방향을 측정된 각도를 나타내며 단위로 (radian, degree)가 있다.
• 높이(z) : 원점으로부터 수직 높이에 대한 거리를 나타낸다.

따라서 점의 위치는 (r,θ,z)로 나타낼 수 있다. 실린더나 원통형태의 구조물을 설명하거나 물리학, 공학, 컴퓨터 그래픽스에서 종종 사용된다.

• 데카르트 좌표계에서 원통좌표계로 변환시 :

$$\begin{gathered} r=\sqrt{x^2+y^2} \\ \theta =ta{n}^{-1}\frac{y}{x} \\ z=z \end{gathered}$$

• 원통좌표계에서 데카르트 좌표계로 변환시 :

$$\begin{gathered} x=rcos(\theta ) \\ y=rsin(\theta ) \\ z=z \end{gathered}$$

구면좌표계(spherical coordinate system)

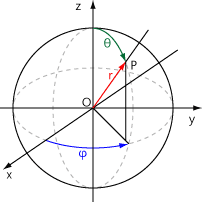
구면좌표계는 점의 위치를 구의 중심으로부터 거리, 방위각, 경도각으로 정의하는 좌표시스템이다. 3차원 공간에서 정의되며 구 형태로 점을 배치하는데 사용한다.

• 반지름(r) : 구의 중심에서부터 점의 위치까지 거리를 나타낸다.
• 방위각(θ) : x축 양의 방향으로 부터 시계 방향으로 측정된 각을 나타낸다. 마찬가지로 일반적으로 radian 단위를 이용한다.
• 경도각(φ) : x-y 평면으로부터 시계방향으로 측정된 방위각을 나타낸다. 이 또한 일반적으로 radian 단위로 표현된다.

따라서 점의 위치는 (r,θ,φ)로 나타내며 구면좌표계는 구 형태의 한점을 나타내므로 지구나 태양같은 천체를 분석하기에 유용하다. 천문학 분야에서 자주 사용됨.

• 데카르트 좌표계에서 구면좌표계로 변환시:

$$\begin{gathered} r=\sqrt{x^2+y^2+z^2} \\ \theta =arccos\frac{z}{r} \\ \varphi =arctan\frac{y}{x} \end{gathered}$$

• 구면좌표계에서 데카르트 좌표계로 변환시:

$$\begin{gathered} x=rsin(\theta )cos(\varphi ) \\ y=rsin(\theta )sin(\varphi ) \\ z=rcos(\theta ) \end{gathered}$$

Euler Angle

그렇다면 로봇에서 언급되는 Euler Angle은 무엇일까?, Euler Angle은 강체의 방향을 3차원 공간 좌표계의 회전으로 이해한다. 데카르트 좌표계와 같이 사용되며 오른쪽 사진과 같이 현재 위치를 대문자(X,Y,Z)로 표현되면 ψ(프사이), θ(세타), φ(로)로 표현할 수 있다.

• ψ(프사이) : z축을 회전축으로하여 x-y 축이 이루는 평면이 회전된 각
• θ(세타) : 회전된 x축(N축)을 회전축으로 하여 z-y축이 이루는 평면이 회전된 각
• φ(로) : 회전된 z축(Z축)을 회전축으로 하여 x-y축이 이루는 평면이 회전된 각

또한 다른 방법으로 해당 축에서의 회전만 고려한 방법으로 X축으로의 회전은 roll, Y축으로의 회전은 pitch, Z축으로의 회전은 yaw라고 부른다.

추가로 Euler와 Quaternion 의 차이는 다음 포스트에 작성할 예정이다.